Bending Strength of the Laterally Supported Beam

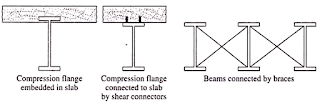
Laterally Supported Beam
– In general, a beam that does not move nor rotate laterally is termed as “Laterally Supported Beams”. This lateral restraint can be possibly obtained
by several means. Few of them are,

Determining the
bending strength of the laterally supported beam is quite straight forward, before
moving into it, let’s get ourselves clear about the failure modes for the
laterally supported beams, from which we can understand which factor governs
the bending strength of the beam.

A typical laterally
supported beam could fail by anyone of the following failure modes:

·        
Shear failure of the
section

·        
Flexural failure of
the section (bending failure)

·        
Web crippling/web
buckling (local failures)

·        
Deflection

Of the above-mentioned
failure modes, Flexural failure of the section is a bending failure, occurs
when the applied load produces an internal bending moment, which is pretty much
higher than the bending strength or moment capacity of the beam.

If we look into the
above statement, there are two important terms,

1.    The internal bending moment generated because
of the applied load.

2.    Bending or Moment capacity of the beam.

The first one can be
determined by simple mechanics. For example, if we have a laterally supported
pinned beam of length L and which supports a uniform load of W kN/m. Then the
bending moment produced will be WL*L/8.

Our main interest is
the Moment capacity of the section. It depends upon the cross-section of the
beam as well as material grade.

In general, the Moment capacity of the section equals the product of Section Modulus and Yield
strength of the material.

M = Z * fy * (factor of safety as per the specified code)

Thus, we have our
required bending capacity or strength of the section.